Introduction
There are various harmful factors that threaten human health (Khoshakhlagh et al., 2022, 2023). Traffic collisions pose a significant risk to global health, with approximately 1.19 million fatalities annually due to road-related injuries or disabilities for an estimated 20 to 50 million individuals (Pourabdian et al., 2020; WHO, 2023). The primary demographic affected by traffic-related deaths is individuals between the ages of 15 and 44 years. Without effective interventions to address road safety, it is anticipated that deaths will continue to rise. Moreover, vehicular crashes rank as the ninth most common cause of mortality across all age groups on a global scale and are expected to become the seventh leading cause of death by the year 2030, according to research by Bendak et al. (2022).
The Kingdom of Saudi Arabia (KSA) spans an expanse of approximately 2.25 million square kilometres. Over the past forty years, the nation has witnessed a sixfold increase in its population, culminating in a total of 36.9 million inhabitants as of 2023 (World Bank Group, 2024). Concurrent with this demographic expansion is prolific economic growth and development through its oil industry that has led to an elevated standard of living and increase in professional immigrants who make up over a third of the KSA population (Bendak et al., 2022; Mansuri et al., 2015). This growth has resulted in substantial changes to road infrastructure and the increase of motor vehicles. The extent of the asphalt-covered roads has expanded from a mere 239 kilometres in 1952 to 64,632 kilometres today. Similarly, the number of registered motor vehicles escalated from 145,000 in 1970 to an estimated 18 million, with around 800,000 additional vehicles being imported annually (Al-Ghamdi, 1999; Bendak et al., 2022; Mansuri et al., 2015).
In 2021, 6,035 people died as a result of crashes on the roads (WHO, 2023). Riyadh region is at the top in terms of the number of traffic crashes, followed by Makkah and Sharqiya region in the second and third places, but in terms of the number of deaths in crashes, Makkah takes the first place (Al-Turaiki et al., 2016; Mansuri et al., 2015). The main contributing factors in crashes are the non-observance of the speed limit law, non-fastening of seat belts, use of alcoholic beverages while driving, and non-use of child seats.
An important step in the prevention and control of crashes is to evaluate and analyse the problems and accurately draw the existing problems so that the necessary planning can be done to contain them (WHO, 2014). As it is obvious, the world around humans is full of complexities. A model is an abstract representation of the components and connections of a phenomenon that shows the relationships between entities and different variables of that phenomenon (Birta & Arbez, 2013).
One of the suitable statistical methods for analysing data recorded in a period of time and at ordered points of time is time series models in which the order of observations is important (Cryer & Chan, 2008). Within time series analysis, the Autocorrelated Integrated Moving Average (ARIMA) model encompasses a more extensive framework compared to the Autocorrelated Moving Average (ARMA) model. These analytical tools are employed to enhance comprehension of time series or to forecast future values. They are applicable to datasets that exhibit stationarity. In this case, with one-time differentiation (corresponding to the “integrated” component), the non-stationary nature of the data is eliminated and the possibility of estimating an ARIMA in the new data is created (Hernandez-Matamoros et al., 2020; Mills, 1990).
Typically, the ARIMA model is represented by the ARIMA (p, d, q), with p, d, and q being non-negative real numbers that signify the degree of the autoregressive, integrated, and moving average parts, respectively. These models play a crucial role in the Box-Jenkins methodology for analysing time series data. When any of these parameters is zero, the model is often referred to by its specific component, such as AR for autoregressive, I for integrated, or MA for moving average. For instance, I(1) corresponds to an ARIMA model with parameters (0,1,0), while MA(1) can be expressed as ARIMA (0,0,1) (Hernandez-Matamoros et al., 2020; Mills, 1990). This model was applied to forecast traffic crashes and consequences including all types of injuries (fatal and nonfatal) due to these crashes in several countries.
In England, Yixuan et al. (2014) predicted the number of driving crashes, the death rate, and the number of vehicles involved. Their results showed that the time series helped to improve the prediction accuracy of the model as a reference for decision-making in the traffic management department. In Colombia, Rodríguez (2015) modelled the process of traffic crash injuries and proposed the ARIMA model for this purpose. The time series model (1,1,0) (5,1,2) showed a good fit to the data and the results provided useful information about the complications caused by traffic crashes in similar areas. In Erbil city in Iraq, Abdulqader et al. (2020) used ARIMA time series models to present the model of people injured in crashes on the road and the ARIMA model (1,0,1) (0,1,1) was chosen as the most suitable and best model. Their results showed that the number of injured people from traffic crashes is decreasing. In the Amhara region of Ethiopia, Getahun (2021) modelled crashes on the roads, including injuries and fatalities from 2013 to 2017. The best models for the injured were ARIMA (1,0,0) (2,0,0). ARIMA (2,0,0) was chosen for fatality crashes and ARIMA (1,1,1) (2,0,0) was chosen for all crashes. Results showed a non-decreasing trend of crashes.
In 2014, Avuglah et al. conducted a study on the number of crashes in Ghana, in which they used the ARIMA time series model to study the trends and patterns of driving crashes. The results showed the upward trend of crashes and the ARIMA model (0,2,1) was recognised as the best model (Avuglah et al., 2014). In 2021, Husin et al. used the Box-Jenkins and state space model for forecasting Malaysia road crash cases and concluded that the basic structural state space model with trend and seasonal components was the most appropriate model (Husin et al., 2021). Hassouna et al. (2020) analysed road crash traffic trends in Palestine using the ARIMA model and observed a generally increasing trend, which is expected to continue in the future.
Sabenorio et al. (2023) also forecasted road traffic crashes in metro Manila using ARIMA modelling and they concluded that despite the decrease in total road crashes, the ratio of road crashes resulting in injuries drastically increased during the lockdown due to reckless driving behaviours. Dutta et al. (2020) applied the ARIMA model for forecasting road crash deaths in India and found that the trends of road crashes and the yearly total number of deaths due to these crashes in this country are upward. In another study, Dutta et al. (2021) forecasted the number of road crashes in India using the Box-Jenkins time series model and concluded that the number of these crashes is increasing (Husin et al., 2021).
In this study, the ARIMA model was used to model the injury consequences (fatal and nonfatal) of traffic crashes in KSA in the period 2002-2022.
Methods
This retrospective study was conducted in 2022 in KSA. The Saudi open data portal, which is a National e-Government Portal, was used to obtain data.[1] As providing access to government data obtained momentum around the world, the KSA was not far behind, providing data from the national portal and the Ministry of Economy (Elbadawi, 2012). The National Open Data Portal permits access, download, and use the data of the KSA ministries and government agencies (AlRushaid & Saudagar, 2016). The data on the injury outcomes (consequences) and car crashes from 2002 to 2022 were extracted from the database. It should be noted that the data from 2002 to 2015 were used to develop the model and the data from 2015 to 2022 were applied to check the validity of the model. Hassouna and Al-Sahili (2020) in a study on practical minimum sample size for road crash time-series prediction models proved that the use of a sample size less than 50 is practically acceptable.
The ARIMA model, conceived by Box and Jenkins in 1970, is extensively applied in forecasting diverse variables. This approach encompasses a three-stage iterative method that consists of choosing the appropriate model, estimating its parameters, and verifying the model’s adequacy. Contemporary interpretations of this methodology advocate for an initial phase of preparing the data, followed by a concluding phase where the model is used for forecasting purposes.
The methodology consists of several steps. First, data preparation is conducted to stabilise the variance and transform the data into a stationary series through differencing. Various tests can be employed to ensure the stationarity of the data, such as the Augmented Dickey-Fuller (ADF) test. Next, in the model suggestion stage, potential models are identified based on the patterns observed in the data. The autocorrelation function (ACF) and partial autocorrelation function (PACF) are examined to determine suitable models. It is crucial to build the model around the suggested order, considering multiple models with different orders if necessary. Following that, in the model selection stage, appropriate criteria are applied to select the best-fitting model. Measures of goodness-of-fit such as AIC (Akaike Information Criterion), AICc (corrected Akaike Information Criterion), and BIC (Bayesian Information Criterion) are utilised for this purpose. Models with significant values and lower AICc, AIC, and BIC values are considered preferable. Additionally, adequacy checks for fitted models are performed using Modified Box-Pierce (Ljung-Box) Chi-square statistics and four plots: histogram of residuals, normal plot of residuals, residuals versus fits plot, and residuals versus order plot. The normality of residuals is examined using the Kolmogorov-Smirnov test.
Once a model with white noise residuals is obtained from these stages, it can be used for forecasting. The accuracy of the model is compared to that of competing models, and the final model chosen for forecasting should demonstrate higher accuracy. To validate the fitted model, actual observations are plotted alongside predicted values for a specific time. Additionally, the accuracy of the model can be assessed using metrics such as Root Mean Square Error (RMSE), mean absolute percentage error (MAPE), mean absolute scaled error (MASE), and R squared. Ofori et al. (2021) have suggested interpretations for MAPE values: less than 10 percent indicates highly accurate forecasting, 10-20 percent indicates good forecasting, 21-50 percent indicates reasonable forecasting, and 51 percent and above indicates inaccurate forecasting. For MASE, the values of lower than 1 are acceptable (Ofori et al., 2021). The statistical tests were carried out using Minitab software.
Results
Table 1 represents the descriptive statistics of the studied variables from 2002 to 2022. Figure 1 also shows time series plots of these variables. The results show that the number of crashes and consequences increased from 2002 to 2022. However, the consequences per 1,000 crashes are decreasing. Given that the consequences per 1,000 crashes have a better trend compared to the variables of crashes and consequences, the ARIMA model was drawn for this variable.
Figure 2 shows plots of the consequences per 1,000 crashes from 2002 to 2015, including a time series plot, a Box-Cox plot, and a time series plot of the first difference. The results showed that the values of this variable do not need transformation. The values of λ for this variable were acceptable. To obtain a stationary series, the researcher took the first differences of data to remove trends from the series. Figure 2 shows a non-stationary behaviour of the first differenced data for this parameter. Also, the Augmented Dickey-Fuller test to the first differenced data reveals that the values of P value for this parameter was less than 0.05 (P<0.001). This implies that the first difference in the testing data is stationary.
Figure 3 displays functions, including the autocorrelation function (ACF) and partial autocorrelation function (PACF), for the consequences per 1,000 crashes. The autocorrelation function (ACF) and partial autocorrelation function (PACF) were examined to identify potential models. The suggested orders are used to build the model. Based on the results, the values of autocorrelation for the studied parameters were significant in the first lag. The value of the partial autocorrelation for the parameter of consequences per 1,000 crashes was significant in the first lag.
Table 2 describes the suggested ARIMA models for the consequences per 1,000 crashes and their accuracy measurements. Based on the results, the ARIMA (0, 1, 0) model had significant model values and the lowest values of AICc, AIC, and BIC. Therefore, these models were selected for forecasting the studied parameters. Next, the researcher checked the adequacy of the fitted models.
Table 3 represents Modified box-pierce (Ljung-Box) Chi-square statistics for Lag (12) of the selected ARIMA models. The results indicated that the Ljung–Box statistics are not significant at any positive lags for the model.
Figure 4 depicts the plots of the histogram of residuals, the normal plot of residuals, residuals versus fits, and residuals versus order for confirmation of the selected ARIMA model. It is observed that the standardised residuals plot of the model is independently and identically distributed with one outlier. There is no evidence of significance in the autocorrelation functions of the residuals of the model and the standardised residuals appear to be normally distributed. The results of Kolmogorov-Smirnov showed that the residuals have normal distributions (P > 0.05).
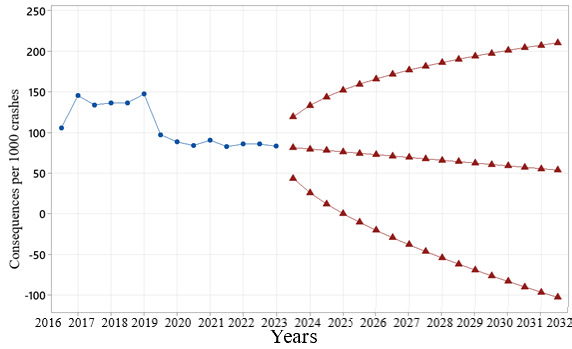
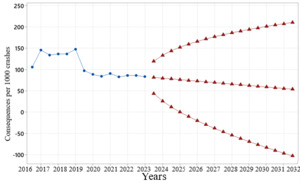
Figure 5 indicates the trend of the consequences per 1,000 crashes to 2032. Table 4 reports the actual values versus forecasted values of this variable. As a result, it is observed that the forecasted number of consequences per 1,000 crashes due to driving in KSA will be decreased in the period to 2032.
To check the validity of the fitted model, the actual observations are plotted with predicted values from 2016 to 2022 (7 years). The results revealed that the total number of predicted values is a nearly equal and exact pattern with the actual data and the actual observations were also within the prediction limit (95%). Based on the values of MAPE, forecasting was highly accurate for consequences per 1,000 crashes. Also, the values of R squared, RMSE, and MASE were acceptable. Therefore, it may be concluded that the proposed model would be a good fit to forecast the parameter of consequences per 1,000 crashes and is well-fitted to forecast the studied parameter.
Discussion
This study analysed the data of traffic crashes and consequences from 2002-2022 using the ARIMA algorithm to process an anticipation model, and afterward applies the data of these years for rectification and analysis, at last, the anticipation for the studied factors is carried out until 2032. According to the findings, although the trend of crashes was upward, the number of consequences per 1,000 crashes will be downward in the years to 2032 (Fouda Mbarga et al., 2018; Khoshakhlagh et al., 2021; WHO, 2015).
There is a relationship between socioeconomic status and injuries from road crash with higher rates in low- and middle-income countries (WHO, 2023). While the KSA is a high-income country, wealth is not evenly distributed across different regions, creating different socio-economic groups within the same country. Greater attention to the safe system principles and the different demographic groups within the KSA is needed to prevent serious crashes on the roads.
Based on the results, the number of deaths per 1,000 crashes due to driving in KSA, the modelling predicts a decrease in the years to 2032. In addition to direct, road safety measures, this may also be achieved through improved post-crash responses (e.g., fire and relief teams are well-trained and the system is equipped with advanced equipment (Al-Zabidi et al., 2022)). Moreover, the safety of vehicles has increased in recent years.
Furthermore, another reason could be the improvement of the health system in KSA. Improvements in the health system in KSA in recent years are also likely to help in post-crash care. This includes increased recruitment of medical personnel and advanced equipment for hospitals (Salami & Bhatti, 2022) for improved pre-hospital care (Ansari, 2004). The pre-hospital emergency system, aims to provide timely services to injured and needy patients, including from traffic crashes, and plays an important role in reducing the consequences of these crashes. Therefore, analysing traffic crashes over a period of time, helps to predict future trends. Based on that, officials can act properly for the development and proper equipment of pre-hospital emergency centres (Cryer & Chan, 2008).
A study in Iran by Yousefzadeh-Chabok et al. (2016) investigated the trend and predicting the number of crashes, in which the ARIMA seasonal model (1,1,3) (0,1,0) was selected as the best model. The results showed the downward trend of death and injuries caused by crashes which are consistent with the findings of this study which the total number of predicted values are nearly equal and follow an exact pattern of the actual data. However, the difference in the results of the mentioned studies on the number of crashes and consequences can be because of cultural, economic and social differences in different countries.
Based on the values of MAPE, forecasting was highly accurate for consequences per 1,000 crashes. Also, the values of R squared, RMSE, and MASE were acceptable. Therefore, it may be concluded that the proposed model would be well fit to forecast the parameter of consequences per 1,000 crashes. As a limitation, data on detailed information related to traffic crashes were not available. Also, it must be noted that ARIMA has very good accuracy for short-term forecasting, but less accurate for long-term forecasting.
Conclusion
This study analysed the data of traffic crashes and consequences from 2002-2022 and used the ARIMA algorithm to process an anticipation model, applied the data of these years for rectification and analysis, and projected the studied factors to 2032. According to the findings, although the trend of crashes was upward, the number of consequences per 1,000 crashes is forecast to decrease in the years to 2032. It may be due to preventive or mitigation measures by various organisations. Although the measures performed for reducing consequences in KSA are useful, necessary measures are also required to decrease traffic crashes considering the increase in population. Also, plannings are necessary to accelerate the slope of reducing consequences due to crashes. Based on the results, the ARIMA method has vigorous performance and high precision for forecasting the consequences of traffic crashes. Therefore, it can be used to forecast the consequences of various crashes in different countries. It is recommended that time series analysis is performed for various types of traffic crashes for more precise investigations. Moreover, it is suggested to plan interventional measures and forecast their effectiveness using this model.
Acknowledgements
The author thanks everyone who helped to perform this study.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors
Human Research Ethics Review
The investigations involving human data were carried out following the rules of the World Medical Association Declaration of Helsinki regarding ethical principles for research involving human subjects.
Data availability statement
Data used in this study are de-identified, open source and publicly available.
Conflicts of interest
The author declares that there are no conflicts of interest.
__consequences_(b)__and_consequences_per_1_000_crashes.png)
.png)


__consequences_(b)__and_consequences_per_1_000_crashes.png)
.png)